1 线性变换

1.1 变换

所谓函数, 不过是一种变换. 更具体一点, 我们可以认为: 函数 变换 映射; 函数是数集 (的子集)到数集(的子集)的映射, 而变换是自身到自身的映射

考虑函数 , 他接受一个参数 , 其中 , 并输出唯一的结果, 是一一对应的关系.

变换亦是如此, 只是自变量不再拘泥于数集. 对于线性变换, 其将向量 作为自变量, 并输出向量.

变换一词在暗示你用运动的思维去思考.(引用自3B1B)

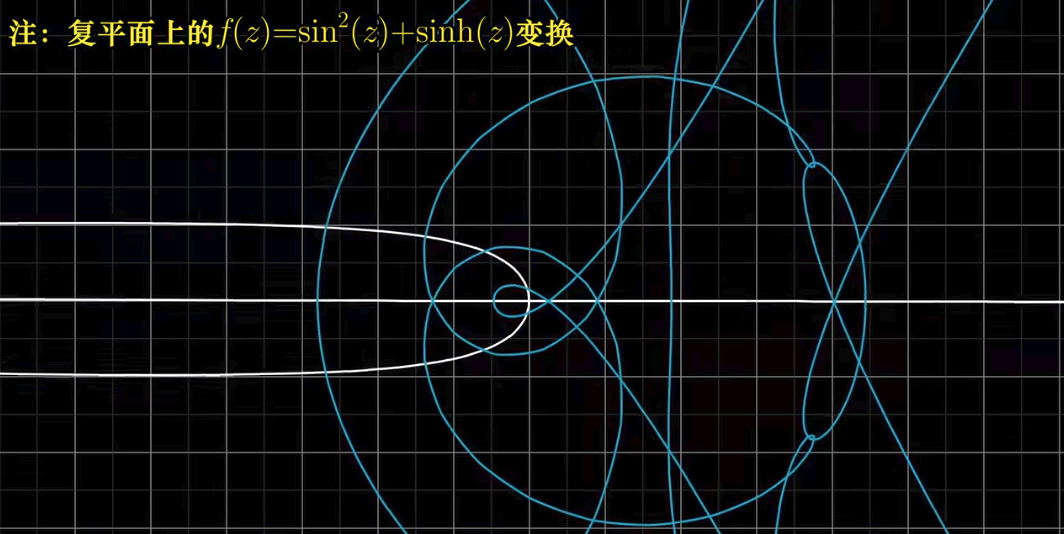
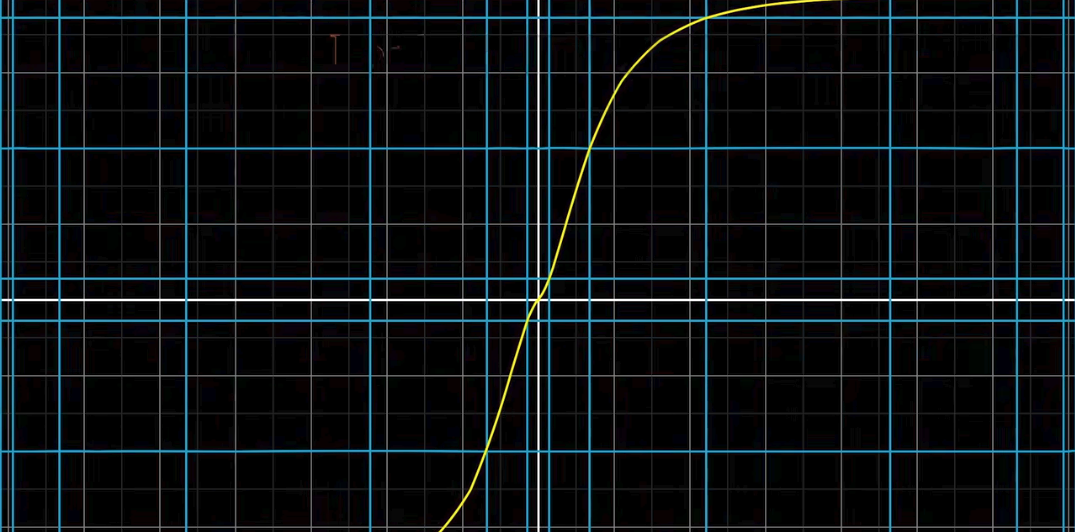
线性代数中的变换即是自身为向量的变换.当所有向量都按照一种方式运动, 所得结果即为变换的结果.(怎么像一句废话🙃)下图分别为普通线性变换, 复变函数(将复数 视作复平面内的向量 )

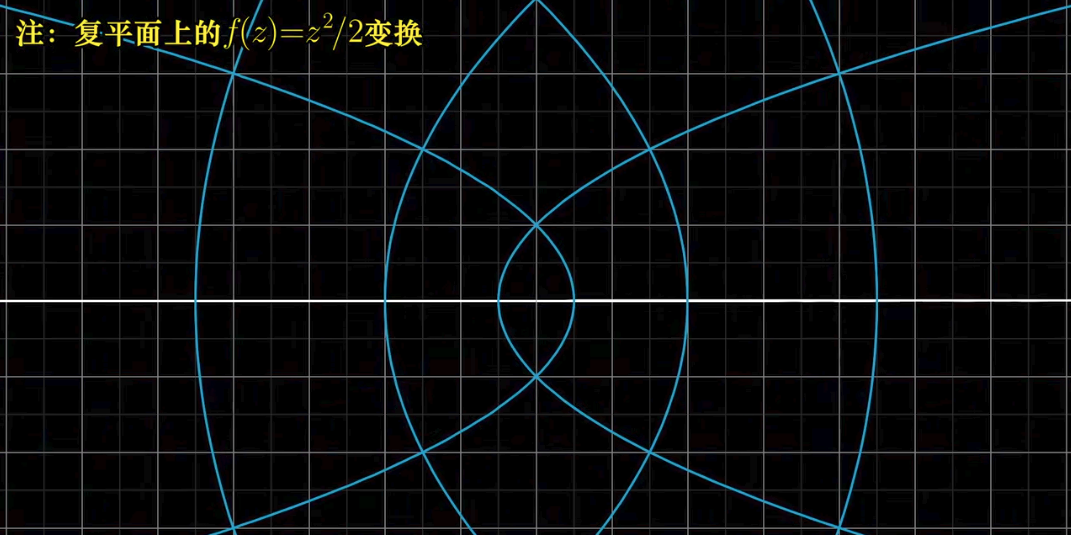
有人可能会问: 诶为什么函数也写在变换里呢?上文提到过, 函数可以看作是特殊的变换, 只不过其自变量和因变量都是数而已, 而复数可以视作向量, 因此复变函数也可以视作线性变换.

1.2 线性变换

若我们要在一个变换上添加线性这一特性, 其需要符合直仍直, 原仍原, 即:

• 直线在变换后仍为直线, 不能弯曲
• 原点在变换后仍为原点, 不能移动

举个例子, 考虑下图中的变换:

其看似符合了条件, 但是若我们考虑原先 方向的向量, 在变换后, 其显然弯曲了, 因此不是线性变换.

一言以蔽之, 线性变换后的结果应使网格线保持平行且等距分布.

如果已经对矩阵的各种意义烂熟于心, 不会真有这种大牛来看我的笔记吧, 那么可以跳过矩阵章节, 直接看三维线性变换章节

2 矩阵

矩阵常常因为其在线代中的重要位置而常常被人们忽略其实际应用与几何意义

由于矩阵相关的计算在各版本的线代相关的书籍中都是重点, 因此本文不会重点关注于此

2.1 矩阵的引入

上文介绍了何为线性变换, 接下来的问题是: 该如何描述一个线性变换?

一个很巧妙的思路是由基向量引出的: 在之前的博客中我们提到了一组基向量决定了一个坐标系, 该坐标系的所有向量均能由该组基向量线性表示.

举个例子: 考虑一组基向量: 和 , 对于 . 若我们改变基向量, 将他们全都放大2倍, 即 , 则 仍然成立. 可以看到, 变换后的向量与变换后的基向量线性组合关系依然成立, 换句话说, 我们可以只根据变换后的 和 来确定变换后的所有向量.

这时候如果我们把 和 合并, 得到 , 这就是最基本的矩阵, 我们把这个矩阵称为2 矩阵, 这个矩阵中存储的是一个线性变换的信息, 仅此而已. 通过这个矩阵和给定的向量, 我们可以求出变换后的向量, 举个例子:

仅有一列的矩阵形式事实上代表的是向量

熟悉矩阵乘法的应该清楚这事实上就是矩阵乘法, 然而更重要的是这事实上就是上文中所讲的将基向量进行线性变换后再数乘的过程

2.2 常见的矩阵

2.2.1 逆时针旋转90

当一个坐标系逆时针旋转 时, 其基向量也逆时针旋转 , 即 , 因此其对应的矩阵为

2.2.2 逆时针旋转

由逆时针旋转 的矩阵 , 利用小学二年级就学过的单位圆我们可以推导出逆时针旋转 时, , 因此其对应的矩阵为

顺时针旋转直接将 取反即可, 追求美观的话则用诱导公式诱导一下就好了捏

算了还是贴一下吧: 顺时针旋转对应的矩阵为

2.2.3 列线性相关

不得不提的是, 当 线性相关时, 其对应的线性变换将将所有向量压缩至一条直线上, 这一点在之后的博客中会详细讨论.

2.3 按照线性变换理解矩阵的意义

说得现实一些, 以后的矩阵乘法, 行列式, 基变换和特征值等概念会更易于理解

2.4 矩阵的基础运算

矩阵的运算满足分配律, 结合律, 交换律

为防止后续缺少理论知识, 在这里简单说一下矩阵的基础运算(加乘)

2.4.1 矩阵加法

矩阵加法与向量加法类似, 直接对应元素相加即可(要求矩阵的维度相同)

2.4.2 矩阵数乘

矩阵数乘与向量数乘类似, 每个元素相乘数字即可

矩阵加法和数乘显然满足交换律, 结合律, 分配律, 使用简单的数乘以及加法即可证明

与文章主体无关, 但是注意行列式中的数乘是每一行/列向外提一次, 即

2.5 矩阵乘法

大多数时候, 如果丢掉矩阵, 设计矩阵的证明可以缩短一半. ——埃米尔·阿廷

2.5.1 维度相同的矩阵乘法

矩阵乘矩阵与向量乘矩阵类似, 但是要注意的是, 矩阵乘矩阵的顺序是有讲究的, 即先乘左边的矩阵, 再乘右边的矩阵. 而且矩阵乘矩阵的维度是有要求的, 即左边的矩阵的列数必须等于右边的矩阵的行数. 例如上文矩阵乘向量的例子中, 左边的矩阵的列数是2, 右边的矩阵的行数也是2, 因此可以相乘

矩阵乘矩阵的运算规则是: 左边的矩阵的每一行与右边的矩阵的每一列对应元素相乘再相加, 例如:

建议不要死背公式, 而是按照线性变换基向量重新线性组合的思路去理解

2.5.2 矩阵乘法的几何意义

不妨设想一下, 若是先进行一次逆时针旋转 , 再进行一次顺时针旋转 , 那么其效果应该就是逆时针旋转 , 写成矩阵表达的形式就是:

先算小括号内的矩阵乘法, 得到:

由此, 我们: 1. 得到了三角函数的加(减)公式 2. 将先顺时针旋转 , 再逆时针旋转 的效果简化为了逆时针旋转 , 并用矩阵加以验证

这个复合变换需要从右往左读, 即先顺时针旋转 , 再逆时针旋转 , 这可以类比小学就学过的复合函数, 与 是不一定相同的

再举个例子, 对于先进行一次线性变换 , 再进行一次线性变换 , 尝试不依赖几何视角来计算这个复合变换的结果

首先考虑原来的基向量 去哪儿了, 经历 后, 其显然变换到了 , 再经历 后, , 同理, , 因此复合变换的矩阵为

忘记怎么理解相乘的去这里复习!

若是想要其较为鲁棒的结论, 此处贴出大致的推导过程, 也是矩阵乘法按列展开, 即将矩阵的每一列与另一个矩阵的每一行对应元素相乘再相加的由来.

对于矩阵 , , 则

题外话: 不难发现矩阵乘法的过程中体现出了很强的迭代行为, 哪怕维数上升或是矩阵数增加, 其本质还是将矩阵的每一列与另一个矩阵的每一行对应元素相乘再相加, 而计算机对于迭代具备先天的优势, 因此矩阵乘法在计算机中有着广泛的应用

2.5.3 矩阵乘法的性质

• 交换律, 对于不同的矩阵 , 不要被上文中简单的旋转变换误导. 考虑 (剪切), (逆时针旋转 ), 则无论是粗暴计算验证或是 想象几何变换的过程, 我们都能发现

• 结合率, 尝试证明 , 显然设出矩阵暴力迭代是可行的, 但是显然一点都不具有欣赏意义, 我们尝试使用变换相继作用的思想去理解, 前者的效果是 , 形象描述就是先进行 , 再把 打个包, 放一起算, 后者的效果是 , 形象描述就是先把 打个包, 放一起算, 再进行 , 显然, 由于相对变换次序不变, 因此二者是等价的

  我第一次看到这个证明的时候, 有些难以理解, 原因是受到了小学老师的影响, 一直认为括号里的先算, 导致错误地认为结合律同样需要改变运算的相对先后次序, 从而搞混了结合律和交换律的本质, 一言以蔽之, 交换律是交换运算的相对顺序, 而结合律是打包计算, 不改变顺序

• 交换律, 由于 的过程是简单的, 因此可以直接代入矩阵乘法中进行证明, 即

3 三维线性变换初探

3.1 线性变换的记录

对于高维, 可视化效应可能没有那么明显, 但是三维依旧是目前可以研究的维度.

与二维类似, 我们依旧可以通过记录三个基向量 , 并将其变换后的结果整合至一个3×3的矩阵中来描述三维线性变换

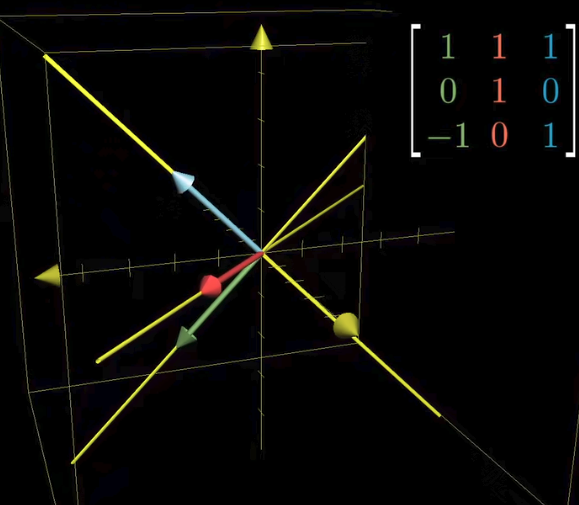
其实到三维之后的线性变换从几何来看就已经没有那么直接了, 至少不太能一目了然, 举个例子, 这是 的变换效果

若是想要通过几何视角理解三维线性变换, 尽量不要在脑子里渲染视频中那种不断旋转的坐标系, 大脑的显卡显然没有那么水平, 而是使用固定视角的右手系为宜

3.2 线性变换结果

与二维中的线性变换类似, 三维中的线性变换结果仍旧可以视作变换后的基向量的线性组合, 即 , 其中 是变换矩阵, 是变换前的向量, 是变换后的向量

3.3 三维甚至更高维度的矩阵计算

3.3.1 矩阵乘向量

使用基向量线性组合的视角不难得到, 对于 , 其结果为 , 即

3.3.2 矩阵乘矩阵

对于 , 其结果按列展开就是 , 即