写在前面

首先对于在现代学习过程中给予我莫大帮助的 3Blue1Brown (3B1B) 表示诚挚的感谢!

其次明确此系列博文的目的: - 不同于对于大学线代课程的预习, 这些文章的目的主要在于揭示线代的简明性, 并在前人的基础上加以自己的理解, 从而尝试提出更为初等的理论 - 是对于3B1B视频的理解以及自己的总结, 并在某种程度上减少今后再次查阅视频所消耗的时间

最后声明

若未特殊说明，本文所提到的一切概念默认在二维/三维直角坐标系中 本文属于学习笔记范畴，请确保文章仅用于学习交流目的，对于其中内含的3B1B视频中的结论、观点以及截图，若有侵权请联系删除

0.线代环境

0.1 线代应用方面

很多人(包括我自己)跟着教材初学线代时对于线代这个东西的作用一头雾水, 极为抽象的概念(如行列式, 矩阵, 特征值等)连珠炮似的砸过来, 很容易造成只会计算却不懂得应用的情况.

线代归根结底依旧是工具, 因此在学习之初明确其应用场景就显得尤为必要

简而言之, 线代较为广泛地被应用在: - 计算机科学 (主要是人工智能训练架构中) - 物理学 (主要是发挥矢量相关作用) - 数学 (主要是多维数据之间潜在的关系的推演中)

0.2 侧重方面

线性代数, 即使名称中含有代数, 但不妨碍几何仍旧是其重要的组成维度之一. 理解坐标系中的几何意义对于熟练运用线代工具, 并深究其本质有着不可或缺的作用

更重要的是, 当今时代计算机已经能接管所有计算领域的工作, 人类在纯计算方面毫无竞争力, 因而理解其几何本质是经验性知识, 有助于不被计算机所代替

1.向量

也许前几章有些无聊, 让人可能有种”显然”的感觉, 但这些视角和思维方式是后续集合讨论的基础.

1.1 应用

与0.1内所述方面相同, 我们先观察向量这一工具在不同领域中的使用 - 物理 (主要关注的维度是向量的长度与方向, 可任意平移) - 计算机 (向量数字类型列表) - 数学 (似乎是最简单的定义, 可以代表任意事物, 仅需保证相加与相乘的结果有意义)

1.2 认识向量

箭头

在初步认识向量时, 我们可以将其认为是以起点为原点的箭头, 这与任意角的初步认识很像 > 值得一提的是, 这里的箭头与上文中所提到的物理学中的向量有所不同的地方在于此处的向量起点恒为原点, 不可任意平移

有序列表

考虑向量 (也可以写作 ), 此处的2和3告诉了我们如何从原点出发到达 的终点, 即分别沿着和轴走2, 3个单位长度.

不难发现, 每一对数都对应有且仅有一个箭头, 反之亦然, 并可由此推广至高维

1.3 向量基础运算

向量的加乘已经驾轻就熟, 但若是我们以一个新的视角看待这两个运算, 我们会发现:

加法

在线代中, 加法几乎是唯一一种情形允许向量的起点离开原点 在计算以原点为起点的向量 时, 我们通常会将 的起点平移至 的起点

这样做法其实暗含了一种思维过程: 将向量视为一种运动, 二者相加即代表运动的叠加, 且运动的先后不影响最终终点, 若再拆分得细一些, 我们可以认为结果事实上是在 方向上分别移动两个向量中的第一个和第二个数, 且运动不分先后

数乘

运用相似的思路, 我们同样可以重新看待向量的数乘

所谓数, 在线代中指的是和矢量不同的: 标量, 他们最大的区别在于后者没有方向, 仅有大小 (长度).

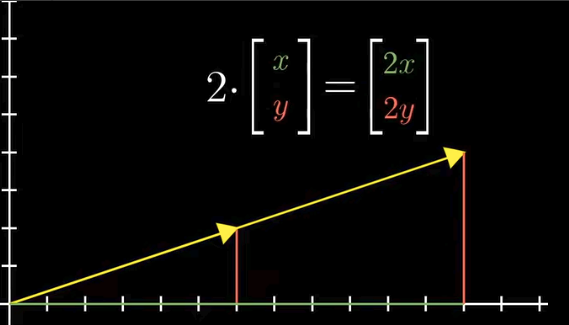
当一个向量乘以一个标量时, 由于后者没有方向, 因此最终的结果向量方向与原向量相同, 仅在长度上乘以那个数, 效果便是将该向量拉伸/缩短了. 借助相似三角形的证明, 可以发现长度变化其实就是将向量的每个维度的大小都乘上对应的数值

需要承认的是, 每个人都有自己看待向量的方式, 但无论何种方式, 相加与数乘永远是独特的两种计算

线代的核心并非是一种观念垄断环境, 而是在于各种观念间的转化理解, 就如同几何与代数之间的转化: 其为计算机提供了操作空间与几何的能力, 同时也为人类透过数据表面窥探其背后的意义与价值的能力

2.基向量、线性组合与线性相关

2.1 基向量

考虑向量 , 通过应用上文中提到的相加与数乘, 我们可以得到

此时不难发现, 对于 , 我们能体会到在这个二维直角坐标系中所有的向量都可以写成 的形式, 此时, 便被称为该坐标系的一组基

基的选择

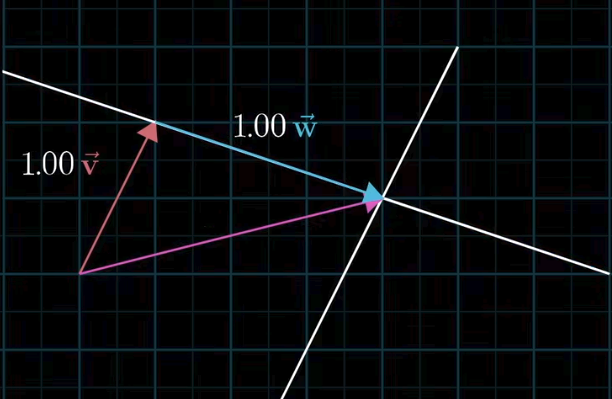
若我们不选择上述的 作为基底, 而是选择平行的 呢?

我们发现, 该组”基底”并无法组成平面内的所有向量, 最有力的证明方式便是举反例: 如 , 要求 的组合, 我们可以列出如下方程:

我们发现, 上述方程组无解, 原因是第一个方程实际上就是 , 与第二个方程矛盾了

由此我们猜测: 平行向量无法作为基底 (未完待续)

2.2 线性组合

对于上文中提到的表达式

我们把这种仅有两个向量的加法与数乘运算的式子称为两个向量的线性组合 (无论向量平行与否) > “线性”的几何体现是固定或不动, 则线性组合结果必为一条直线(相对于二维平面), 推广至高维如三维则是: 结果必为一个平面(甚至一条直线) >

2.3 张成的空间

在基底确定时, 所有的线性组合分为两种情况: - 大部分情况下, 最终的结果可以到达空间(平面)中的每一个点 - 然而就像上文中选择的那组平行基底一样, 有些情况下(比如平行), 结果向量的终点仅能形成过原点的一条直线 - *其实还有一种, 若均为 , 则结果仅包含原点

对于上述所有的线性组合, 我们称其为该组基底所张成的空间.若我们联系上文所提到的基础运算, 那么此时该组基底所张成的空间便可以被描述为该组基底仅通过基础运算所获得的所有可能向量的集合

若将视线拓宽至三维空间, 那么选择两个基底 后(假设他们不平行), 所张成的空间应为一个面, 而此时再加上一个基底 , 就又分为两种情况: - 若 的终点不在那个平面上, 那么通过k的伸缩可以将该平面拓宽至整个三维空间 - 反之所张成的空间仍停留于这个面

2.4 线性相关

在先前的案例中, 无论是二维空间中平行的向量还是三维空间中终点共面的向量, 我们发现移除某个向量后, 剩下的向量所张成的空间不变, 那么我们称这组向量是线性相关的

一组向量是线性相关的, 当且仅当:

• 移除某个向量后, 剩下的向量所张成的空间不变
• 某个向量可以表示为其他向量的线性组合, 即其已经落在其他向量所张成的空间中
• 也可以认为 个向量张成的空间在维度上退化了至少一个维度

反之, 我们称这组向量是线性无关的, 当且仅当 不, 其中 不全为0且 , 使得

特别提醒, 线性无关和线性独立略有不同.前者的强调的是个体向量间, 后者强调的是整个向量组

由此我们可以填好2.1的坑了. 基的严格定义为: 向量空间的一组基是张成该空间的一个线性无关的向量集